I’ve heard a few times from friends that they’re repeatedly surprised to discover they don’t actually understand how transformers work as well as they had thought. Here’s a simple exercise I did for myself that I think helped a lot (though with the obvious caveat that I am presumably subject to a similar bias to overestimate my understanding ;) )
To do this, you should have an understanding of the transformer architecture - there are millions of tutorials that teach this and you’ll profit by studying them - if you want to spend some time reflecting on it, the famous “A Mathematical Framewok for Transformer Circuits” is very good. Also, the transformers circuit thread also includes these exercises. I haven’t done more than glanced at them, but they’re doubtless quite good.
The final goal of these exercises is to design your on induction head. An induction head is one that does “AB…A—>B”. We’ll be using two self-attention layers with no MLPs. The simplification that makes this fun is that you’re allowed to completely abstract away the residual stream : you are allowed to write and query arbitrary semantic information about a token into its residual stream, respecting locality and causality.
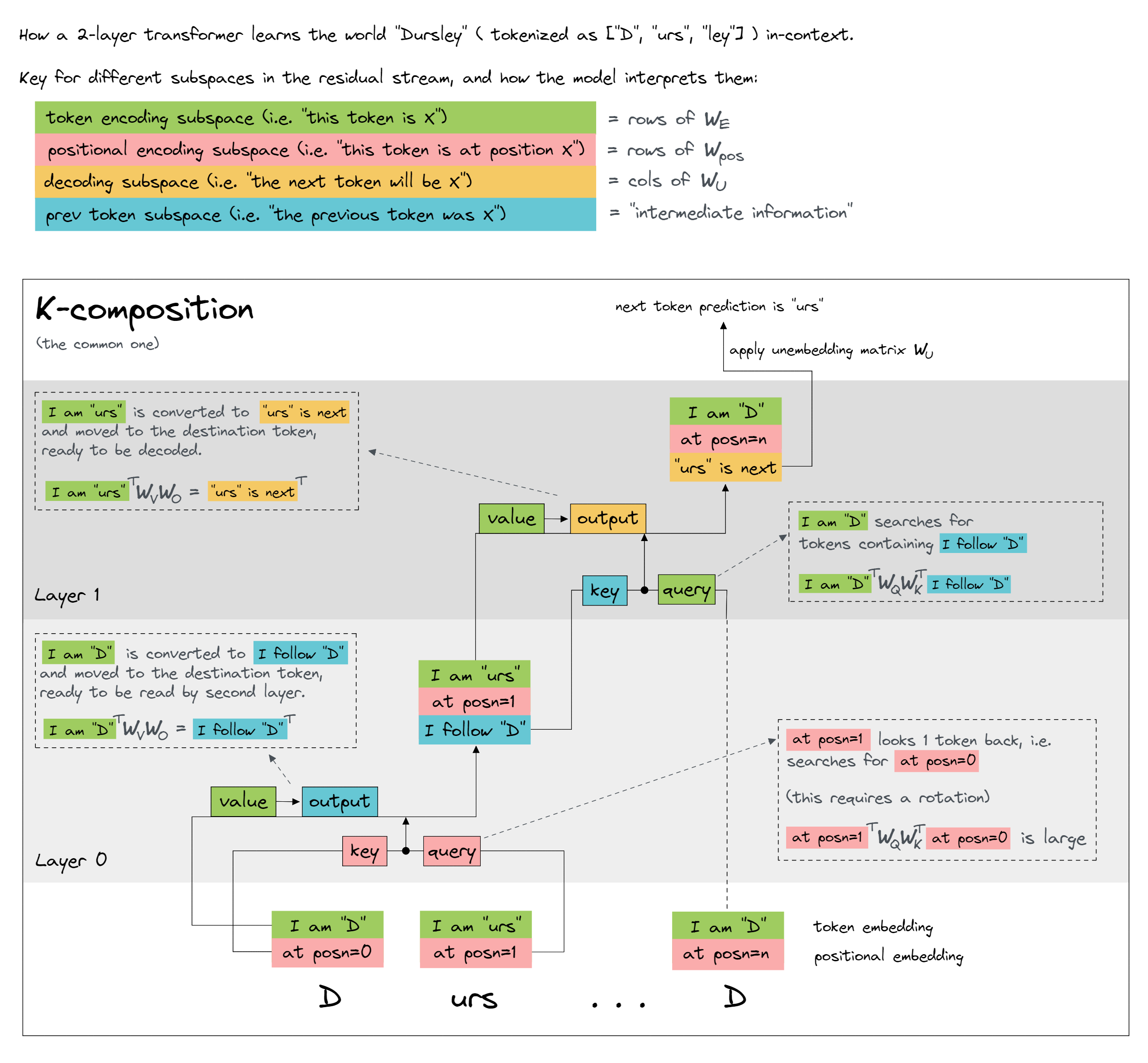 This image from ARENA 1.2 “Introduction to Mechanistic Interpretability” explains it perfectly; it depicts an induction process which does “AB….A –> predict B”.
This image from ARENA 1.2 “Introduction to Mechanistic Interpretability” explains it perfectly; it depicts an induction process which does “AB….A –> predict B”.
Your job is to write out the Q, K, V, and O matrices! (also take a look at the consequent QK and OV products)
Exercises: Try doing each of these WITHOUT and then WITH a positional encoding, to get a feel for exactly how they work and don’t. You should assume for all that we use a causal mask (after maybe trying one or two without).
- Write a conditional “IF current token is A, then write B” (“A –> B”)
- Then try “If previous token is A, write B” (“AX –> B”, where it should predict this no matter what single token X is)
- Then try for “if previously ever saw A, then predict B” (“A…X–>B”)
- Try “if previous 2 tokens were AB, write C” (“AB –> C”)
- Try the ‘cycle’ which does “if current token is A then write B, if it’s B then write C, …., and if current token is N, write A.” (4 tokens should be enough : A –> B –> C –> D –> A)
- Lastly, do the induction head. An induction head implements “If current token is A AND previously saw AB THEN write B” (“AB…A–>B”).
NB: It may be hard to get rid of some ‘interference terms’ in the ‘cycle’ exercise, which you should note as qualitatively important, but it doesn’t seem super useful /easy to manually try and design around them. I played with it for 20 minutes and couldn’t figure it out, iirc.
GPT5’s Work for Exercise 1 (yes I checked it and edited it; don’t worry I don’t trust it either)
(some typographical errors with the LaTeX here that I couldn’t iron out - nothing detracting from meaning. ‘Live Laugh Love LaTeX’ right)
Worked Example — Designing “A → B”
We implement: If the current token is A, then write B (“A → B”). Single attention head, single self-attention layer, no MLP. For simplicity, we treat $W_O W_V$ as one combined map $W_{OV}$.
The residual stream is a short semantic tape of flags/symbols read/written “all at once.” You could realize this as a one-hot basis; with more context you might store a list such as [“current_token is A”, “prev_token is X”, …] (not needed here). The downside vs. Turing machines is linear, parallel access rather than a movable head.
1. Semantic encoding
We view encode(token) as a small set (or linear combo) of semantic flags:
- encode(A) → [“current_token is A”]
- encode(B) → [“current_token is B”]
- encode(X) → [“current_token is X”]
2. Weights $W_Q$, $W_K$, $W_{OV}$ (semantic maps)
Goal: fire “is current_token A?” in $Q$, then $W_{OV}$ writes “predicted_token is B”.
Query vector and weight matrix
We define the query vector for a given token as:
\[\vec{q}_{\mathrm{current\_token}} = \mathrm{encode}(\mathrm{current\_token}) \cdot W_Q\]Choose $W_Q$ so only the query for “is current_token A?” can fire:
\[W_Q = \begin{bmatrix} \text{"Q: is current\_token A?"} & 0 & 0 \\ \vdots & \vdots & \vdots \end{bmatrix}\]- If current_token = A:
$\vec{q}_{\mathrm{current_token}} = \big[ \mathrm{Q:~is~current_token~A?} \big]$ (fires strongly). - Else: $\vec{q}_{\mathrm{current_token}} = \vec{0}$.
Key vector and weight matrix
Similarly,
\[\vec{k}_{\mathrm{current\_token}} = \mathrm{encode}(\mathrm{current\_token}) \cdot W_K\]Pick $W_K$ so the key for each token identity sits in a matching position to the query:
\[W_K = \begin{bmatrix} \text{"K: current\_token is A"} \\ \text{"K: current\_token is B"} \\ \text{"K: current\_token is X"} \\ \vdots \end{bmatrix}\]- If current_token = A:
$\vec{k}_{\mathrm{current_token}} = \big[ \mathrm{K:~current_token~is~A} \big]$ - If current_token = B:
$\vec{k}_{\mathrm{current_token}} = \big[ \mathrm{K:~current_token~is~B} \big]$ - If current_token = X:
$\vec{k}_{\mathrm{current_token}} = \big[ \mathrm{K:~current_token~is~X} \big]$
$W_{OV}$ — combined output–value map
\[\begin{array}{c|ccc} & \text{"QK: current\_token is A"} & \text{"QK: current\_token is B"} & \text{"QK: current\_token is X"} \\ \hline \text{"OV: write predicted\_token is B"} & 1 & 0 & 0 \\ \text{"OV: write seen A recently"} & 0.8 & 0 & 0 \\ \text{noop} & 0 & 0 & 0 \end{array}\]Interpretation:
- If attention locks onto current_token is A, then write predicted_token is B and seen A recently.
- Otherwise, only NOOP.
Some rows store intermediate computations for later use.
3. Attention computation (semantic view)
(note we only consider a ‘one-entry’ attention matrix - we’ll pretend for simplicity that all the other attention goes to the BOS token and does nothing) Easy as cake:
\[\mathrm{score} = \vec{q}_{\mathrm{current\_token}} \cdot \vec{k}_{\mathrm{current\_token}}\]- If current_token = A: dot product large → attention weight $\approx 1$ on self.
- Else: dot product = 0 → weight $\approx 0$.
4. End-to-end semantics
When current_token = A:
- $\vec{q}_{\mathrm{current_token}}$ = “Q: is current_token A?”
- $\vec{k}_{\mathrm{current_token}}$ = “K: current_token is A” → strong match
- $W_{OV}$ fires rules:
- write predicted_token is B
- write seen A recently
Compactly:
\[\mathrm{Output(current\_token = A)} \approx W_{OV} = \begin{bmatrix} \mathrm{predicted\_token~is~B} \\ \mathrm{seen~A~recently} \\ \mathrm{noop} \end{bmatrix} \propto \mathrm{encode}(B) + \mathrm{intermediate~state}.\]